ここで学習すること
決定木の特徴と実装プログラムを学習します。
決定木とは説明変数のひとつひとつに着目し、データ内のある値を境にデータを分割する手法です。
決定木では各説明変数の目的変数へ与える影響度合いが分かります。
決定木は線形分離ができないデータの分離は難しい点がデメリットです。また、学習が訓練データに寄りすぎる傾向があります。
決定木はscikit-learn(ライブラリ)のtree(モジュール)にあるDecisionTreeClassifier()を用います。
irisデータの分類を決定木にて行います。
必要なモジュールをインポートします。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
from sklearn.tree import DecisionTreeClassifier
irisのデータセットからカラム0と2を読み込み、説明変数xと目的変数yを作成します。詳細は機械学習6|ロジスティック回帰で分類を行うを参照ください。
iris = datasets.load_iris()
X = iris.data[:, [0, 2]]
y = iris.target
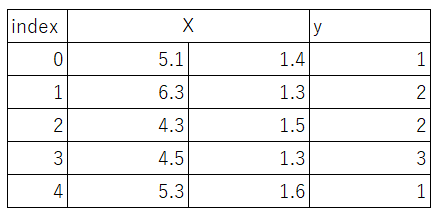
irisのデータセットがこのようになりました
#データを訓練データとテストデータに分割します
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=42)
#決定木のモデルを構築します。
model = DecisionTreeClassifier()
#モデルを使って学習します。
model.fit(train_X, train_y)
グラフ表示を行います。plt.scatter:散布図の作図を行います。横軸にXの0列目、縦軸にXの1列目の値をとります。マーカーサイズはy、マーカー色はcool、グラフの透明度は1(透明ではない)とします。
plt.scatter(X[:, 0], X[:, 1], c=y, marker=”.”,cmap=matplotlib.cm.get_cmap(name=”cool”), alpha=1.0)
x1_min, x1_max = X[:, 0].min() – 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() – 1, X[:, 1].max() + 1
np.arange(x1_min, x1_max, 0.02)でx1_nimからx1_maxを0.02ごとに区切った数列を作成します。同様にnp.arange(x2_min, x2_max, 0.02)でx2_nimからx2_maxを0.02ごとに区切った数列を作成します。ここで作った数列をx軸、y軸としたメッシュグリッドを作成します。
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02))
.reshape(xx1.shape)でZのデータ形式をxx1と合わせます。
Z = model.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)
.contourfでxx1,xx2,Zの等高線を表示します。透明度はalphaで指示します。cmapでグラデーションをWistia*に指示します。
plt.contourf(xx1, xx2, Z, alpha=0.4,cmap=matplotlib.cm.get_cmap(name=”Wistia”))
plt.grid(True)









