ここで学習すること
分類手法のひとつのサポートベクターマシンの使った分類を学習します。
学習結果を散布図で表示します。
サポートベクターマシン(SVM)はロジスティック回帰ど同様にデータの境界線を見つけ分類を行う手法です。サポートベクトル(他のクラスと近いデータの点)からの距離が最大となる位置に境界性を設定します。
ロジスティック回帰にくらべ、境界線が2つのクラス間の離れた場所に置かれるので分類予測精度が向上する傾向があります。ただし、計算量が増えることにより予測に時間がかかります。
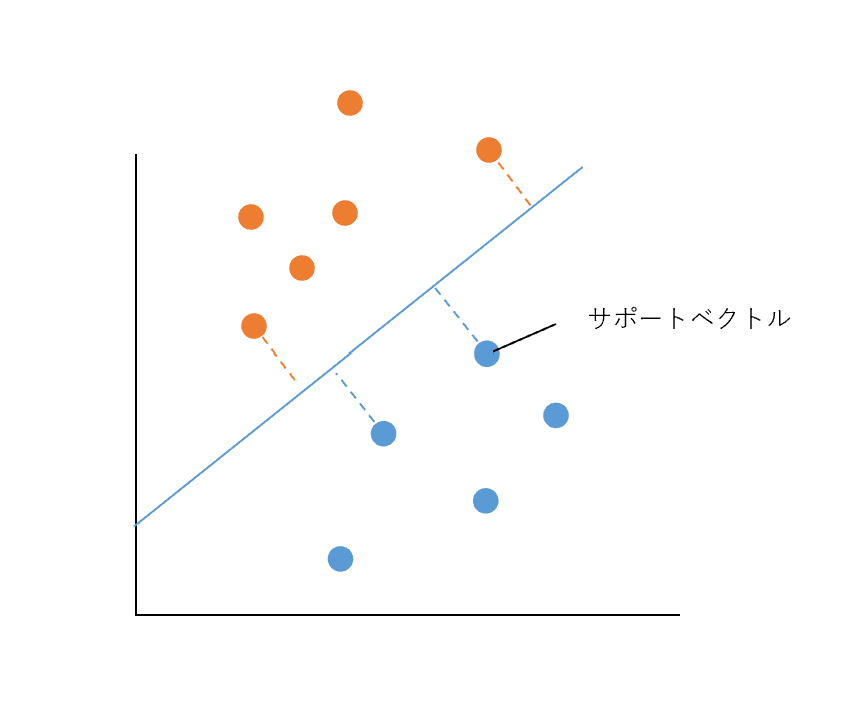
SVMは分類する境界線が2クラス間の最も離れた場所に引かれるため、ロジスティック回帰と比べて一般化されやすく、データの分類予測が向上する傾向があります。
SVMはscikit-learnのメソッドLinearSVM()で実装できます。
pythonに格納されているirisデータをサンプルに使用します。irisデータとは150個のアヤメ(花の一種)のサンプルの「がく片の長さ」「がく片の幅」「花びらの長さ」「花びらの幅」の4つの説明変数と、3種の品種(目的変数)が格納されています。ここでは「がくの長さ」と「花びらの長さ」を使用します。
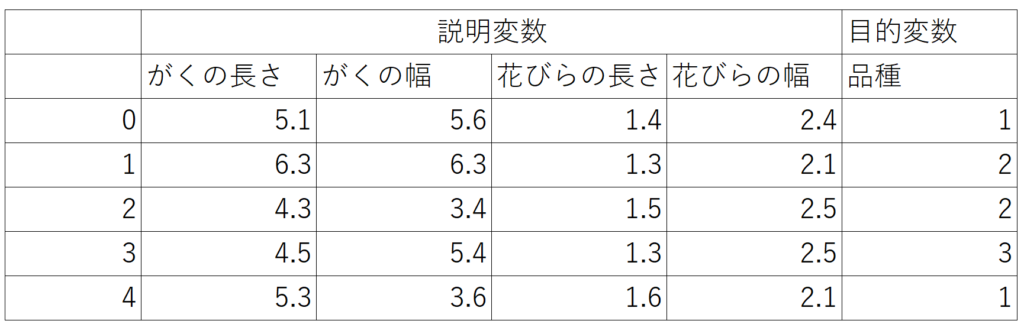
irisのデータセットをインポートします。
from sklearn import datasets #sklearnのデータセットをインポートします
iris = datasets.load_iris() #irisのデータセットを読み込みます
X = iris.data[:, [0, 2]] # irisのindex 0列目(がくの長さ)と2列目(花びらの長さ)を変数Xに格納します(行はすべて格納します)
y = iris.target # irisのクラスラベルを格納
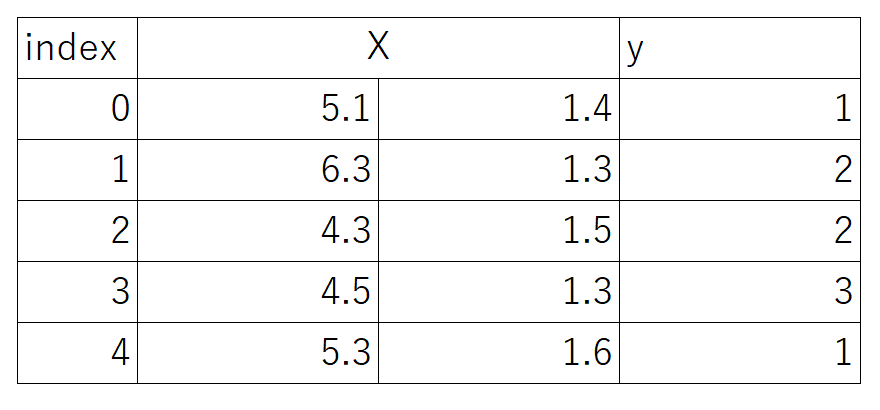
irisのデータセットがこのようになりました
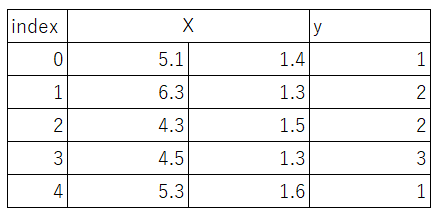
データを訓練データとテストデータに分割します
from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.3, random_state=42)
SVMを構築します
model = LinearSVC() #SVMを構築します
model.fit(train_X, train_y) #モデルに学習させます
model.score(test_X, test_y) #検証データの正解率を出力します
散布図に表示します
import matplotlib #可視化モジュールをインポートします
import matplotlib.pyplot as plt #散布図メソッドをインポートします
import numpy as np #行列モジュールnumpyをインポートします
# .scatterで散布図を作成します。
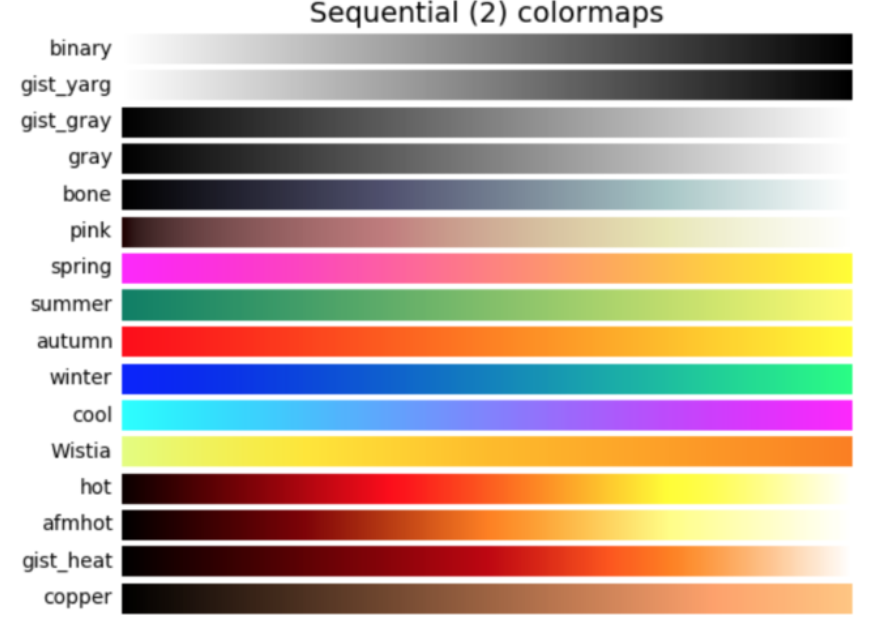
横軸に説明変数Xの第1引数(1列目)、縦軸に説明変数Xの第2引数(2列目)をプロットします。 マーカーサイズはy、マーカー種類は・、マーカー色はcoolの可変を指定します。alpha=1.0とすることでgラフの透明度は0とします。(alpha=0.0の時グラフは透明で見えなくなります)
plt.scatter(X[:, 0], X[:, 1], c=y, marker=”.”, cmap=matplotlib.cm.get_cmap(name=”cool”), alpha=1.0)
x1_minを説明変数Xの第1引数(1列目)の最小値-1、x1_maxを説明変数Xの第1引数(1列目)の最大値+1と定義します
x1_min, x1_max = X[:, 0].min() – 1, X[:, 0].max() + 1
y1_minを目的変数yの第1引数(1列目)の最小値-1、y1_maxを目的変数yの第1引数(1列目)の最大値+1と定義します
x2_min, x2_max = X[:, 1].min() – 1, X[:, 1].max() + 1
np.arange(x1_min, x1_max, 0.02)でx1_nimからx1_maxを0.02ごとに区切った数列を作成します。同様にnp.arange(x2_min, x2_max, 0.02)でx2_nimからx2_maxを0.02ごとに区切った数列を作成します。ここで作った数列をx軸、y軸としたメッシュグリッドを作成します。
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02),np.arange(x2_min, x2_max, 0.02))
.reshape(xx1.shape)でZのデータ形式をxx1と合わせます。
Z = model.predict(np.array([xx1.ravel(), xx2.ravel()]).T).reshape(xx1.shape)
.contourfでxx1,xx2,Zの等高線を表示します。透明度はalphaで指示します。cmapでグラデーションをWistia*に指示します。
plt.contourf(xx1, xx2, Z, alpha=0.4,cmap=matplotlib.cm.get_cmap(name=”Wistia”))
plt.xlim(xx1.min(), xx1.max()) #x軸の範囲をxx1の最小値、最大値とします
plt.ylim(xx2.min(), xx2.max()) #y軸の範囲をyy1の最小値、最大値とします
plt.title(“classification data using LinearSVC”) #グラフタイトルを表示します
plt.grid(True) #グラフにグリッドを入れます
plt.show()
=>
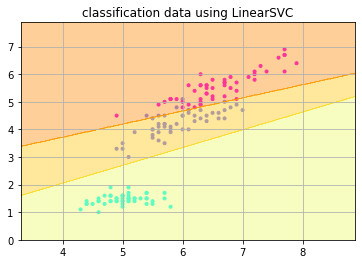
このように1,2,3の品種が3つに直線的に分類されました。
*グラデーションは下図のように名前と色が定義されています。