ここで学習すること
過学習について解説し、過学習を防止しモデル精度を上げるプログラムを紹介します。
モデル精度を表す決定係数について解説します。
過学習
過学習とは過去のデータに合わせすぎて予測精度が上がらないことをいいます。
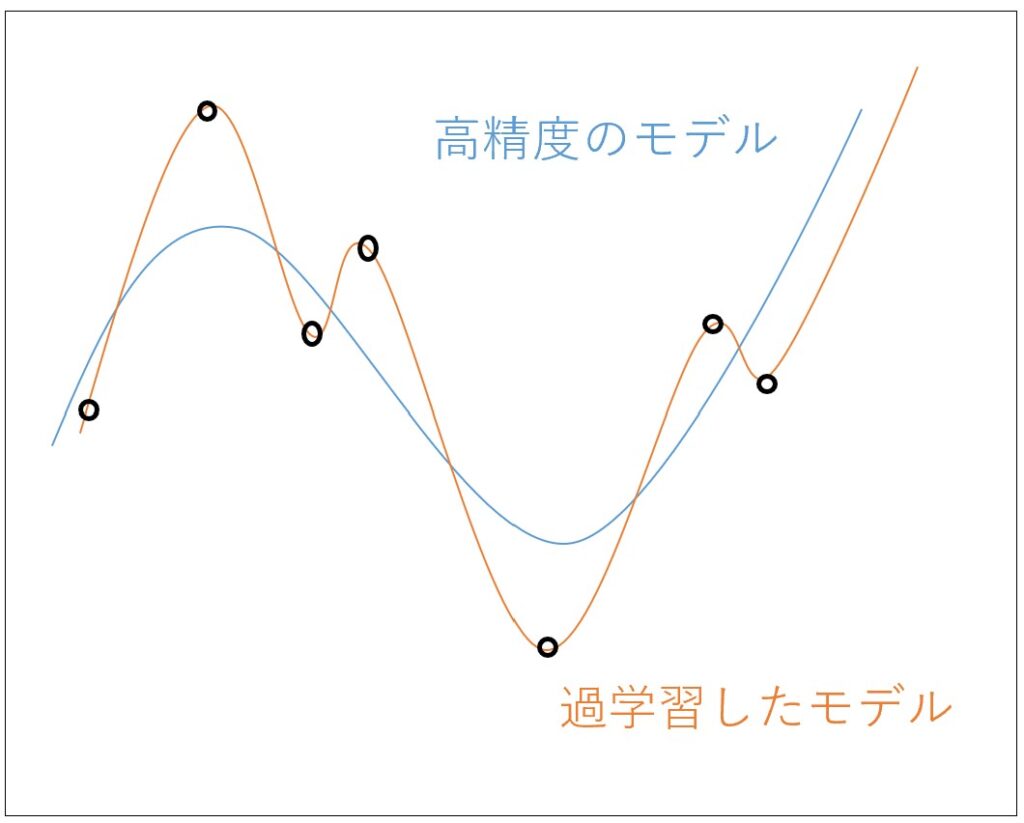
実際は青線に近い現象であっても実際のデータは青線グラフの通りにはならない場合が多いです。
にも関わらず全てのデータを通る曲線を作成しようとすると、予測精度の低いモデルとなります。
正則化
回帰分析モデルに対し、データ同士の複雑さに対しペナルティを加えることで、複雑さを低減することを正則化といいます。
上の赤グラフを青グラフへ修正するイメージです。
L1正則化:予測に対する影響の低いデータにかかる係数を0とする手法。情報がたくさんあるデータの分析に向いている。
L2正則化:係数が大きくなりすぎないよう制限する手法。
Lasso回帰
L1正則化にてパラメータを設定します。pythonでのコマンドは以下です。
model = Lasso()
Ridge回帰
L2正則化にてパラメータを設定します。pythonでのコマンドは以下です。
model = Ridge()
ElastionNet回帰
Lasso回帰とRidge回帰を組み合わせた手法で、コマンドは以下です。
model = ElasticNet()
訓練データにラッソ回帰、リッジ回帰、ElasticNet回帰を適用して精度を検証し、最も精度が良い回帰モデルを採用します。
決定係数
決定係数R^2とは、予測データが実際のデータとどのくらい一致しているかを示す指数のことです。

分子は実際の値と予測値の差で、分母は実際の値と正解の差です。
つまり、決定係数は1以下となり、1に近いほど精度が高いと言えます。
0.8以上であれば精度が良いと言えます。
決定係数は以下で求められます。
R = model.score(test_X, test_y)











