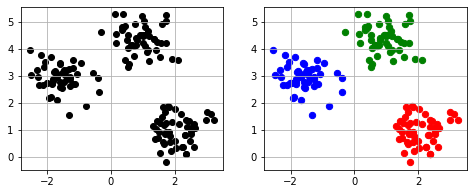
K-means法はデータを分散の等しいn個のクラスターに分ける手法です。各クラスター毎にセントロイドと呼ばれる平均値が割り当てられます。分散の等しいクラスターに分けるにいはSSEという指数を使います。SSEはデータ点とセントロイドの差の二乗和を求めたものです。K-means法はこのSSEをすべてのクラスターで等しくかつ最小化するようにセントロイドを選びます。
1.初めにデータからk個のデータを抽出しそのk個の点を最初のセントロイドとします。その後次の工程を繰り返します。
2.すべてのデータを最も近いセントロイドに振り分けます。
3.各k個のセントロイドに振り分けられたデータの重心を計算し、その重心を新たなセントロイドとします。
1~3を繰り返し新しいセントロイドと古いセントロイドの距離を比較し、その距離が短くならなくなったら計算を終了します。
import matplotlib.pyplot as plt
from sklearn.cluster import Kmeans
from sklearn.datasets import make_blobs
#サンプルデータを100個作ります
X, Y = make_blobs(n_samples=100, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
#K-means法で3つに分類します
km=KMeans(n_clusters=3, random_state=0)
#モデルを使って学習します
Y_km=km.fit_predict(X)
#グラフ枠を定義します。
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(8,3))
ax1.scatter(a[:,0], a[:,1], c=’black’)
ax1.grid()
#プロットします。
ax2.scatter(X[Y_km == 0, 0], X[Y_km == 0, 1], c=”r”, s=40, label=”cluster 1″)
ax2.scatter(X[Y_km == 1, 0], X[Y_km == 1, 1], c=”b”, s=40, label=”cluster 2″)
ax2.scatter(X[Y_km == 2, 0], X[Y_km == 2, 1], c=”g”, s=40, label=”cluster 3″)
ax2.grid()
plt.show()
=>